Integral of $e^{-x^2}$ from $-\infty$ to $\infty$

In this article, I will give a detailed explanation of why the Gaussian integral is equal to $√\pi$, that is, why the following equality holds:

The usual way we go about solving a definite integral $∫_a^b f(x)\,dx$ is as follows:

1. Find a primitive function of $f(x)$, i.e. a function $F(x)$ such that $F’(x) = f(x)$.
2. Calculate $\lim_{x→b-} F(x) - \lim_{x→a+} F(x)$.

Unfortunately, this doesn’t work for $∫ e^{-x^2}\,dx$ for a simple reason: There is no combination of elementary functions that differentiates to $e^{-x^2}$ (which follows from the rather advanced Liouville’s theorem). Fortunately, there is a clever trick that will allow us to calculate the value even without looking for a primitive function, and that’s what we will do for the rest of this article.

First, let’s denote $$ I = ∫_{-∞}^∞ e^{-x^2}\,dx\,. $$ Obviously, changing the letter denoting the variable will not change the value of the integral (we are still integrating the same function), so $$ I = ∫_{-∞}^∞ e^{-y^2}\,dy\,. $$ Multiplying both equations leads to $$ I^2 = ∫_{-∞}^∞ e^{-x^2}\,dx ∫_{-∞}^∞ e^{-y^2}\,dy\,. $$ Now, $∫_{-∞}^∞ e^{-x^2}\,dx$ is just a number (a constant), so we can put it inside the second integral: $$ I^2 = ∫_{-∞}^∞ e^{-y^2} \l(∫_{-∞}^∞ e^{-x^2}\,dx\r)\,dy\,. $$ However, from the point of view of the integral with respect to $x$, $e^{-y^2}$ is also just a number, so we can put it inside, too: $$ I^2 = ∫_{-∞}^∞ ∫_{-∞}^∞ e^{-y^2}e^{-x^2}\,dx\,dy = ∫_{-∞}^∞ ∫_{-∞}^∞ e^{-(x^2+y^2)}\,dx\,dy\,. $$ Now the fun part begins, but we need a little bit of theory of two-dimensional integration. You are probably familiar with the concept of the Riemann integral (or the improved Lebesgue version), which calculates the area under the graph of a function. Under certain conditions that are satisfied in our case (such as when the function is positive and continuous), this area is equal to the definite integral calculated via primitive functions (antiderivatives), so we don’t really have to worry about the interpretation of the integrals above.

Riemann/Lebesgue integration works in the same way in two dimensions (or any number of dimensions, for that matter); only now we are calculating volumes, not areas. Fubini’s theorem tells us that a two-dimensional integral can be split into two one-dimensional ones (if the integral is finite): $$ ∫_{ℝ^2} f(\mathbf{z})\,d\mathbf{z} = ∫_ℝ \l(∫_ℝ f(x,y)\,dx\r)\,dy = ∫_{-∞}^∞ ∫_{-∞}^∞ f(x,y)\,dx\,dy\,, $$ where the notation $∫_{ℝ^2} f(\mathbf{z})\,d\mathbf{z}$ simply means that we are calculating the volume under the graph of $f$ using the two-dimensional Riemann or Lebesgue integral.

Let’s continue our calculation of $I^2$. Using Fubini’s theorem, we can convert the two one-dimensional integrals into just one two-dimensional integral: $$ I^2 = ∫_{-∞}^∞ ∫_{-∞}^∞ e^{-(x^2+y^2)}\,dx\,dy = ∫_{ℝ^2} e^{-|\mathbf{z}|^2}\,d\mathbf{z} $$ (we have used the formula $|(x,y)| = √{x^2+y^2}$, which allowed us to write $e^{-(x^2+y^2)} = e^{-|(x,y)|^2} = e^{-|\mathbf z|^2}$).

Now we only need to calculate the two-dimensional integral $∫_{ℝ^2} e^{-|\mathbf{z}|^2}\,d\mathbf{z}$, and we’re done. But wait a minute – didn’t we start with exactly the same kind of integral, namely $∫_{ℝ} e^{-x^2}\,dx$? How is this all helping?

The point is that we can calculate the same integral in different coordinates, in a way that was impossible in one dimension—we will use the polar coordinate system $\mathbf{z} = (r\cos(φ),r\sin(φ))$, $φ ∈ [0,2\pi)$, $r ∈ [0, ∞)$. The way you calculate volume under the graph of a function $g$ in polar coordinates is as follows: $$ \text{volume under }g = ∫_0^∞ ∫_0^{2\pi} g(r,φ)\,r\,dφ\,dr\,. $$ Notice the term $r$ that wasn’t there in the ordinary Cartesian coordinates. Why is it there now? Of course, there are mathematical ways to prove this, but the reason is quite easy to see if you look at the following picture:

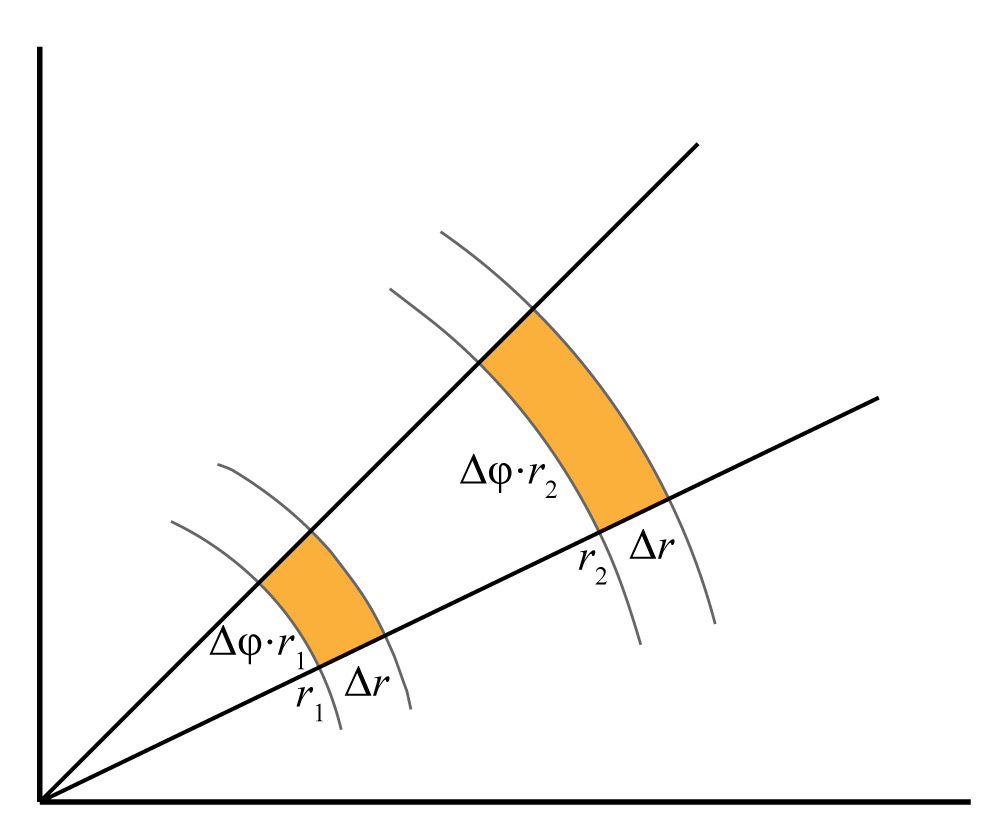
Imagine you are filling the plane with tiny curved rectangles with sides $\Delta r$ and $r\Delta φ$ (the length of a circular arc is the angle times the radius). The volume under the graph of $g$ is approximately the sum of the values $g(r,φ)$ multiplied by the area of the corresponding rectangle, which is $r\Delta φ\Delta r$. The term $r$ will stay there even if you send $\Delta φ$ and $\Delta r$ to $0$ and get the integral.

Recall that we have arrived at the following equation: $$ I^2 = ∫_{ℝ^2} e^{-|\mathbf{z}|^2}\,d\mathbf{z}\,. $$ Luckily, $|\mathbf{z}|^2 = r^2$, so we can calculate the same volume in polar coordinates as $$ I^2 = ∫_0^∞ ∫_0^{2\pi} e^{-r^2}r\,dφ\,dr = ∫_0^∞ e^{-r^2}r ∫_0^{2\pi} 1\,dφ\,dr = 2\pi ∫_0^∞ e^{-r^2}r\,dr\,. $$ Thanks to the $r$ we now have in the integral, we can use a simple substitution $s = r^2$: $$ I^2 = 2\pi ∫_0^∞ \frac{1}{2}e^{-s}\,ds = \pi\l[-e^{-s}\r]_0^∞ = \pi\,. $$ And that’s the end of our journey—we can only conclude that $$ I = √\pi\,. $$