Tip: See my list of the 
MostWhen you learn the traditional western music notation in order to be able to play an instrument, one of the first things you learn is the order of sharps and flats and the scales they correspond to. Students usually memorize that the G major scale has one sharp (F♯), G minor has two flats (B♭, E♭), and so on, without ever learning the logic behind the order of scales and number of accidentals.
Teachers usually “explain” the logic by showing the structure of half steps and whole steps. So you learn, for example, that the C major scale has the structure
where a dot indicates a whole step and no dot indicates a half step. You can see that easily on a piano keyboard (there are black keys between C D E and F G A B but no black keys between E F and B C):
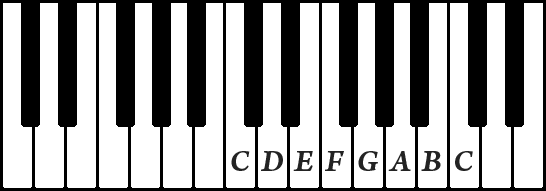
When you start from a different note, say G, but you want the scale to “sound the same” as C major, just a little bit higher or lower, it must have the same order of half steps and whole steps (otherwise playing the scale would produce a different melody). Looking at one of the diagrams above, we see that there is something wrong with the structure when we start with G:
The half step between E and F comes too early (it should be between the last two notes). But we can fix that if we move F a half step up! So we denote the half step above F by F♯ (the black key between F and G) and get
And this is, unfortunately, where most teachers (and most textbooks, for that matter) stop explaining. They just tell you that flats and sharps are used to “correct” the structure when you start from a different note, and then give you a list of scales ordered by the number of flats and sharps, usually depicted as what they call “the circle of fifths”. You are supposed to memorize it without really knowing why.
The full explanation
The purest interval in music (apart from an octave) is the perfect fifth. When you play two tones together that are a perfect fifth apart (e.g. C and G), the result does not sound happy or sad, energetic or melancholic; it sounds neutral. The reason is that their harmonic series overlap to a great extent, but we will not discuss the details in this article.
By going several fifths (and octaves) up or down, you can construct any interval in music. Two fifths up give a major second (e.g. C–G–D), three fifths down give a minor third (e.g. A–D–G–C), and so on (don’t worry if you don’t know what the perfect fifth from a particular note is yet; we will discuss it in detail below).
The more fifths you need to construct an interval, the more dissonant or energetic the result sounds (because the harmonic series overlap less and less). It turns out that:
This is something you should always keep in mind. The diatonic scale (which is just a fancy name for the tones of the major and natural minor scale without saying which one is “first”) is constructed as a series of six perfect fifths, just like in the following diagram (each space indicates a perfect fifth, and the underlined notes are the tonal centres, i.e. the first degrees, of what we call “major scale” and “minor scale”):
This also explains where the most common pentatonic scale comes from; it is just a shorter chain of fifths: C G D A E.
Now, what are accidentals? Let’s say we start the chain of six consecutive fifths from C instead of F. To do that, we need another fifth after B; let’s call it X:
F is gone, and X fills the melodic gap caused by the removal of F, so if we just call it F♯ (F sharp), the melodic order of the letters will stay the same: G A B C D E F♯ G. The diagram then looks as follows (again with tonal centres underlined):
We can do the same on the other side as well. If we end with E, we need one more note on the left, which we can call B♭ (B flat), resulting in the scale F major or D minor:
This gives us the following rule:
We can continue the process in both directions, getting the following line of perfect fifths:
Which scale you are using is determined by which seven consecutive symbols you choose, with the first degrees of major and minor scale being the second and the fifth symbol, respectively, e.g.
And that’s how key signatures work. You just move your selection on the line of fifths to the left or to the right. It is therefore essential to remember how notes are ordered in fifths. Once you remember F C G D A E B, it is easy to derive everything else.
If you want to calculate the signature of E major, for example, you just have to calculate the distance from C to E on the line, which is 4 to the right, so you get 4 sharps. The ordering F C G D A E B also tells you the order of sharps (left-to-right) and flats (right-to-left), which are usually memorized as two completely unrelated things by students.
And what role does the circle of fifths play? The circle of fifths is just the line of fifths drawn as a circle in which F♯ and G♭, respectively d♯ and e♭ for minor scales, overlap. The reason is that they have the same frequency in the most common tuning system used today. This is made possible by reducing the ratio of frequencies in every perfect fifth slightly from 1.5 to approximately 1.4983, which causes the frequencies to start repeating after 12 perfect fifths (i.e. there are only 12 different classes of frequencies).
This is extremely important for practical reasons because otherwise a musical instrument would require a different key, hole or fret for every note, at least the commonly used ones. C♯ and D♭ would be two separate black keys on the piano, separated by about a quarter of a semitone, and the same goes for all other black keys—and that’s just without mentioning double flats and sharps, which some pieces require. This would be a terrible mess.
However, there is, in my humble opinion, absolutely no advantage to imagining the line of fifths as a circle when reading and writing music notation. Accidentals have to be spelled correctly depending on what they represent, and imagining the system as a circle only makes it harder to visualize in your head.
