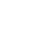 |
Is it possible to divide by zero?
This is a common question on mathematical discussion boards, with people sometimes feeling that mathematicians are too closed-minded for (...)
June 7, 2014 – Jakub Marian – Mathematics
|
 |
Calculus of finite differences without variables
This article contains an elementary introduction to calculus of finite differences. Instead of working with a variable, say $n$, it uses a (...)
May 8, 2014 – Jakub Marian – Mathematics
|
 |
Definite integration without variables
In the previous article, we discussed how to integrate functions without using variables, but only in the case of indefinite integration. (...)
April 23, 2014 – Jakub Marian – Mathematics
|
 |
Quantification without variables
I have written several articles about a way to do classical calculus without using variables, e.g. how to differentiate or integrate (...)
February 15, 2014 – Jakub Marian – Mathematics
|
 |
Second substitution method for integration without variables
This article is based on my article about integration without variables which you may want to read first in order to understand what’s (...)
February 1, 2014 – Jakub Marian – Mathematics
|
By the way, have you already seen my brand new web app for non-native speakers of English? It's based on reading texts and learning by having all meanings, pronunciations, grammar forms etc. easily accessible. It looks like this:
 |
Indefinite integration without variables
In this article, I’ll assume you have already read my article on differentiation without variables. Just as a quick reminder: $\iota$ (...)
January 12, 2014 – Jakub Marian – Mathematics
|
 |
Integral of $\cos^2(x)$
Let’s use integration by parts: If we apply integration by parts to the rightmost expression again, we will get $∫\cos^2(x)dx = ∫\cos^2(x)dx$, which is not very useful. The trick is to rewrite the $\sin^2(x)$ in the second step as $1-\cos^2(x)$. Then we get (...)
November 24, 2013 – Jakub Marian – Mathematics
|
 |
Render LaTeX in Wikipedia using Mathjax
Let’s face it—mathematical expressions rendered as images look ugly, especially in inline formulas. Also, if you, like me, have all (...)
|
 |
Differentiation (derivatives) without variables
To be able to differentiate a function without using variables, we have to be able to denote the function we want to differentiate without (...)
October 14, 2013 – Jakub Marian – Mathematics
|
 |
How to define functions without using variables
First, note that this article is not about the definition of elementary functions, such as $\sin$ and $\cos$, and operations, like $a^b$, (...)
October 11, 2013 – Jakub Marian – Mathematics
|